Что такое парадокс?

«Это парадокс», «это парадоксально»… Ежедневно мы слышим и произносим подобные фразы. Но достаточно ли отчетливо представляем себе их суть? В этой статье мы подробно разберем тему парадоксов и попробуем понять, что это за явление.

Простой классический парадокс — это утверждение, которое следует логике, но противоречит здравому смыслу. Представьте фразу: «Это утверждение ложно». Как вы считаете, сама по себе она выражает правдивую или ложную мысль? Любой ответ на этот вопрос приводит к смысловому противоречию. Предположим, что утверждение истинно, но ведь само оно сообщает нам ровно противоположную мысль. Если же утверждение ложно, то на самом деле оно должно сообщать нам, что является истинным. Так как фраза ссылается сама на себя, возникает смысловой замкнутый круг.

Иногда парадоксы выходят за рамки логики и затрагивают философию, математику или даже физику. Но так или иначе в большинстве случаев основу парадокса составляет несостоятельный аргумент, который загоняет слушателя в мыслительную ловушку. Однако часто именно парадоксы указывают на несовершенство научных знаний и помогают решать сложные задачи.

История парадоксов

История парадоксов в значительной степени отражает историю развития самого человеческого мышления. Она уходит корнями в античную Грецию, где формировались многочисленные научные школы, связанные с философией, логикой и математикой. Первым философом, который начал формулировать парадоксы, считается Зенон Элейский, живший в V веке до н. э. Он делал это не из желания поупражняться в риторике, а стремился показать несостоятельность фундаментальных концепций пространства, времени, движения и множественности. Для этого он использовал апории (прим. ред.: от древнегреческого «ἀπορία» — «безысходность») — логически верные рассуждения, приводящие к абсурдным выводам. Приведем 2 известные апории Зенона, которые дошли до нас благодаря пересказам Аристотеля.

• «Дихотомия» (деление пополам) — апория, показывающая парадоксальность концепции движения. Если некто хочет пройти до конца дороги, сначала ему необходимо преодолеть половину пути, но до того — 1/4, 1/8, 1/16, 1/32 и так далее до бесконечности. Так как любое расстояние можно разделить пополам, придется выполнить бесконечное количество действий, следовательно, путешествие может даже не начаться, а любое реальное движение является иллюзией. На похожих аргументах строится известная апория, согласно которой Ахиллес никогда не сможет догнать черепаху.
• «Множественность» — апория, ставящая под сомнение идеи о пространстве и множествах. Если какой-либо объект обладает размером, значит, его можно разделить на части. Но и каждая из этих частей также будет иметь величину и может быть разделена на более мелкие элементы. Продолжая этот мысленный процесс, мы видим парадокс — бесконечное количество малых частей создает конечную величину. 

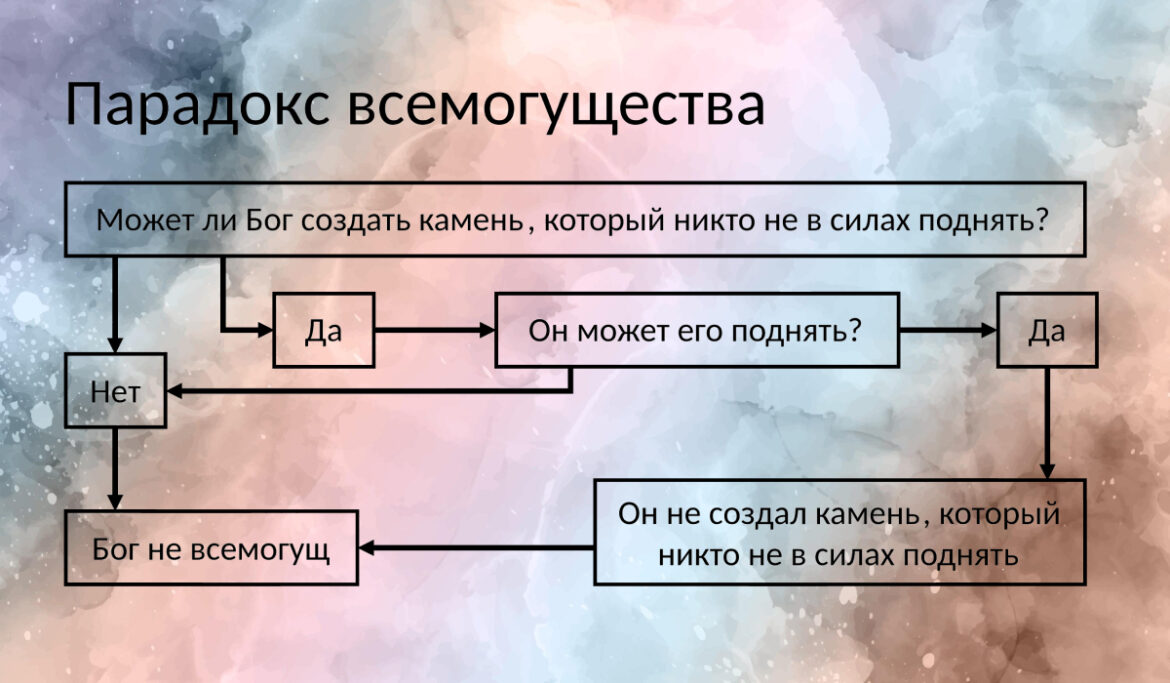
В эпоху Средневековья смыслы парадоксов все чаще смещаются в сторону толкований религиозных доктрин. Примерно в VI веке нашей эры начинает зарождаться целая группа «парадоксов всемогущества». Среди множества разных версий самой известной является следующая: «Может ли Бог создать настолько тяжелый камень, который сам не сможет поднять?». Утверждение представляет собой логический тупик. Если всемогущее существо может все, то может ли оно поставить себя в такие условия, в которых сделать что-либо ему станет не под силу?

Всплеск научного интереса к парадоксам пришелся на начало XX века. В 1901 году британский математик и философ Бертран Рассел пошатнул основы математики, показав противоречивость любой существовавшей в то время теории множеств. Давайте вспомним общую формулировку парадокса и попробуем объяснить его смысл на жизненном примере. Итак, сам парадокс звучит так: «Для любого четко определенного свойства существует множество всех и только тех объектов, которые обладают этим свойством. Выберем такое свойство, согласно которому множество не является элементом самого себя. Обозначим R как множество всех множеств, которые не содержат сами себя. Если R содержит сам себя, это противоречит указанному выше условию. Если же не содержит, это в той же степени противоречит определению этого множества». Звучит запутанно, не правда ли? А теперь — обещанный жизненный пример.

Не углубляясь в суть математических терминов, приведем популярную аналогию с брадобреем. Представьте город, где был издан указ, согласно которому брадобрей бреет всех и только тех, кто не бреется сам. Если брадобрей бреется сам, он не имеет права этого делать, так как нарушает закон. Если же он не бреется сам, то, согласно тому же указу, обязан брить сам себя.

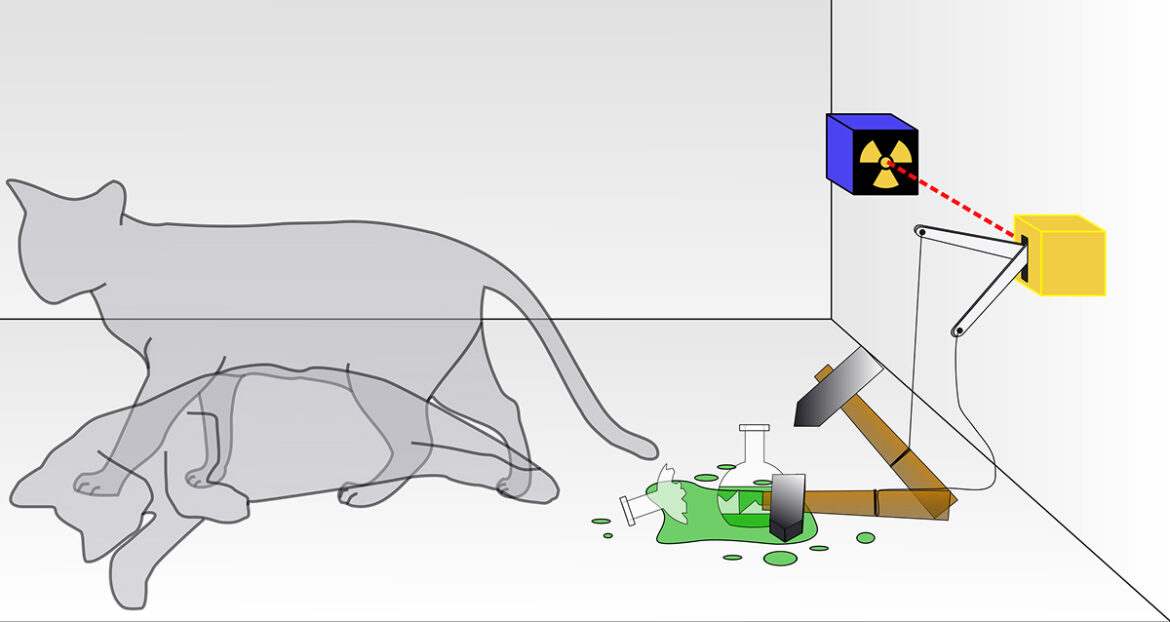
С развитием науки парадоксы вышли за пределы абстрактных мысленных образов и начали проникать в мир реальных явлений. Знаменитый парадокс «кот Шрёдингера» ярко проиллюстрировал конфликт между квантовой физикой и тем опытом, который мы получаем, взаимодействуя с макроскопическим миром. Австрийский физик Эрвин Шрёдингер в 1935 году предложил представить герметичный стальной ящик, в котором сидит живой и здоровый кот. Также внутрь помещен атом радиоактивного вещества, который в течение часа может распасться с вероятностью 50%. Если это происходит, счетчик Гейгера активирует механизм, разбивающий колбу с синильной кислотой, и кот мгновенно погибает. В противном случае кот остается жив.

Парадокс возникает из-за принципа квантовой суперпозиции. Представьте подброшенную в воздух монетку. Пока она крутится, мы не можем однозначно ответить на вопрос: «Орел или решка?». То есть монетка как бы находится в двух состояниях одновременно до тех пор, пока мы не поймаем ее и не увидим результат. Так же и в квантовой суперпозиции — пока система не наблюдается, радиоактивный атом находится одновременно в целом и распавшемся состояниях. И только в момент измерения из всех вероятных состояний атома система будто выбирает одно, которое «представляет» наблюдателю.

Шрёдингер стремился показать неполноту квантовой теории через пример, который невозможно себе представить в реальном мире. Следуя принципу квантовой суперпозиции, кот в ящике является и живым, и мертвым одновременно. Парадокс «кота Шрёдингера» заставил ученых всего мира задуматься о роли наблюдателя при определении свойств реальности.

Виды парадоксов

Американский математик, логик и философ Уиллард Ван Орман Куайн рассматривал парадоксы не как логические курьезы, а как серьезные научные проблемы, требующие анализа и разрешения в рамках отдельных теоретических систем различных наук. В 1962 году он предложил классификацию парадоксов, выделив 3 основных вида.

• Истинные парадоксы — утверждения, которые противоречат интуитивному опыту, но не логике, и при детальном анализе оказываются правдивыми. Например, нам кажется странным, что в группе из 23 человек вероятность того, что хотя бы у двух из них совпадут дни рождения, составляет 50%, ведь в году 365 дней. Тем не менее в такой группе можно составить 253 уникальные пары (прим. ред.: 22 + 21 + 20 + 19…), что значительно повышает шанс совпадения. В группе из 70 человек формируются 2 415 уникальных пар, и двое родились в один день с вероятностью 99,9%.
• Ложные парадоксы — утверждения, основанные на ошибочных аргументах или логических уловках. К ним можно отнести упомянутый в самом начале статьи «парадокс лжеца», апории Зенона или же распространенный софизм (прим. ред.: софизмы — это формально правильные, но ложные по существу умозаключения): «То, что ты не потерял, ты имеешь. Ты не потерял рога, следовательно, ты рогат».
• Антиномии — утверждения, которые выявляют противоречия в самих общепринятых научных парадигмах или системах понятий. К ним относится парадокс Рассела, побудивший математическое сообщество пересмотреть теории множеств, чтобы исключить подобные противоречия.

Как решать проблему парадоксов

Универсального приема, который помог бы решать любые парадоксы, не существует. Если говорить о классификации Куайна, в истинных парадоксах необходимо самому провести цепочку умозаключений и принять полученные результаты, изменив собственное восприятие окружающего мира. В случае с ложными парадоксами также необходимо провести тщательный анализ, чтобы определить слабое место в рассуждениях. Антиномии же требуют системного пересмотра определений, теорий и аксиом. Сейчас мы с вами постараемся найти решение для каждого упомянутого в статье парадокса.

• «Это утверждение ложно» — в обычном смысле решить этот парадокс нельзя, но его можно нивелировать, изменив «правила игры». Допустимым вариантом является концепция иерархичности языков. Например, на первом уровне мы высказываемся о мире: «Снег белый». А на втором делаем вывод о справедливости высказывания первого уровня: «Фраза «Снег белый» истинна». Таким образом, выражение, ссылающееся само на себя, нарушает иерархический принцип и становится бессмысленным.

• «Дихотомия» — эту апорию Зенона можно решить как математическими, так и физическими методами. Математическим ключом к пониманию являются сходящиеся бесконечные ряды. Проще всего понять эту идею, если представить ряд, в котором 0 последовательно возводится в степени от 1 до бесконечности, а полученные результаты складываются. Каким бы ни было количество элементов, сумма в любом случае будет равна конечному числу — нулю. Обратившись к физике в рамках школьной программы, мы вспомним, что Зенон упускает такие важные показатели, как скорость и время. Разбивая движение на отрезки, он заставляет своих последователей усомниться в непрерывности этого процесса.
• «Множественность» — концепция сходящихся рядов способствует разрешению и этого парадокса, однако апорией множественностей Зенон обозначил один из фундаментальных вопросов мироздания: «Из чего состоит материя и как долго ее можно делить?». В попытках разрешить логическое противоречие древнегреческие философы Демокрит и Эпикур предложили и начали развивать свои теории неделимых атомов, а уже в XX веке усилиями многих выдающихся физиков была разработана Стандартная модель, описывающая элементарные частицы.
• «Парадоксы всемогущества» — такие противоречия решаются не поиском определенного ответа на вопрос, а уточнением самого понятия всемогущества. Отвечая на подобные парадоксы, представители Церкви утверждали, что всемогущество означает не возможность сделать все что угодно, а лишь то, что не противоречит законам логики. Иными словами, всемогущее существо способно делать все, что возможно, а не все, что человек способен вообразить.

• «Парадокс Рассела» — обозначив фундаментальную проблему в теории множеств, Бертран Рассел внес свой вклад в изменение математических концепций. Вместо ответа на вопрос математики создали такие условия, в которых его нельзя было бы задать, — ввели строгую систему аксиом. Ключевым моментом решения стал запрет на самопринадлежность множества. Выражение «множество содержит само себя» в большинстве случаев стало нельзя корректно выразить математическими способами. Вторым важным фактором стало ограничение на создание множества всех множеств. При наличии множества A создавать подмножества можно только из составляющих его элементов.
• «Кот Шрёдингера» — хотя этот парадокс имеет почти вековую историю, общепринятого решения, способного «примирить» квантовый и макроскопический миры, пока что не существует. Одной из наиболее популярных интерпретаций данного мысленного эксперимента является теория декогеренции. Ее суть заключается в том, что такие макроскопические объекты, как кот, счетчик Гейгера и колба с кислотой, не могут быть изолированы от окружающего мира. Они непрерывно взаимодействуют с огромным количеством фотонов и частицами, составляющими молекулы воздуха и других веществ. Столь обширный комплекс взаимодействий приводит к разрушению нестабильной квантовой суперпозиции — декогеренции — а значит атом и, как следствие, кот переходят в одно из состояний независимо от присутствия наблюдателя.

Парадоксы в художественном творчестве

В конце статьи давайте немного отдохнем от логических хитросплетений и отметим, что парадоксы — это мощный инструмент художественного творчества. Когда герои различных произведений произносят фразы, содержащие в себе противоречия, читатели получают возможность подумать о глубине их смысла. Многие подобные выражения вышли за рамки своих литературных источников и стали самыми настоящими афоризмами.

• «Чем меньше женщину мы любим, тем легче  нравимся мы ей» (Александр Пушкин, «Евгений Онегин»).
• «Все животные равны, но некоторые животные равнее других» (Джордж Оруэлл, «Скотный двор»).
• «Чтоб добрым быть, я должен быть жестоким» (Уильям Шекспир, «Гамлет»).
• «Я слышал столько клеветы в Ваш адрес, что у меня нет сомнений: Вы — прекрасный человек» (Оскар Уайльд, «Портрет Дориана Грея»).
• «Чем примитивнее человек, тем более высокого он о себе мнения» (Эрих Мария Ремарк, «Возлюби ближнего своего»).

***

От древних апорий Зенона до квантового «кота Шрёдингера», парадоксы представляют собой нечто большее, чем простые интеллектуальные головоломки. Они выступают в роли инструментов познания, которые стимулируют человеческое мышление выходить за привычные рамки и искать новые истины. Какими бы ни были парадоксы, они помогают науке двигаться вперед и зачастую вносят коррективы в постулаты, которые ранее казались фундаментальными и неприкасаемыми.

Автор текста Иван Стефанов

Изображение на обложке: Freepik