Современная теоретическая химия и физика сталкиваются с фундаментальной проблемой описания квантовой динамики сложных молекулярных систем. С одной стороны, строгое квантово-механическое описание движения ядер в молекулах чрезвычайно точно, но практически неприменимо для реальных систем из-за того, что с увеличением числа степеней свободы вычислительные затраты растут экспоненциально. С другой стороны, классическая механика сравнительно «недорога» с точки зрения вычислений, однако не способна воспроизвести важнейшие квантовые эффекты, такие как интерференция, нулевая колебательная энергия и туннелирование. Над этой пропастью между точностью и реализацией вычислений ученые уже несколько десятилетий строят «мост» полуклассических методов, которым стремятся соединить преимущества обоих подходов.
Одним из наиболее широко применяемых полуклассических методов является пропагатор Германа-Клука (Herman—Kluk propagator), предложенный Майклом Германом и Эриком Клуком в 1984 году. Он используется для описания временной эволюции квантовых волновых пакетов, особенно в молекулярной динамике и спектроскопии, и позволяет учитывать важные квантовые эффекты, используя при этом ансамбль классических траекторий.
Его ключевая идея состоит в том, что квантовая динамика может быть аппроксимирована ансамблем классических траекторий, каждая из которых снабжена специальной фазой и амплитудным множителем, учитывающими квантовые эффекты. В рамках этого подхода динамика волнового пакета выражается как интеграл по фазовому пространству, где вклад каждой траектории осциллирует с фазой, определяемой классическим действием. Это и становится главным препятствием для вычислений: при росте размерности системы статистическая сходимость метода резко ухудшается, и прямое применение пропагатора Германа-Клука становится практически невозможным.
Для преодоления этой трудности были предложены различные модификации, одной из которых является так называемая клеточная фильтрация или фильтрация Филинова (Filinov filtering). В стандартной версии этого подхода фазовое пространство разбивается на ячейки конечного размера, а вклад всех траекторий внутри одной ячейки аппроксимируется аналитически на основе поведения центральной траектории. Это позволяет существенно уменьшить осцилляции подынтегрального выражения и улучшить статистическую сходимость расчетов.
Однако у стандартной клеточной фильтрации имеется принципиальный недостаток: размер ячеек вводится как внешний параметр, не связанный напрямую с числом используемых траекторий. В результате даже при бесконечном числе траекторий метод не гарантирует сходимости к исходному пропагатору Германа-Клука, а исследователю приходится дополнительно анализировать зависимость результата от ширины ячеек, что увеличивает вычислительные затраты и снижает концептуальную строгость метода.
В журнале «The Journal of Chemical Physics» опубликована статья ученых из Института химических наук и инженерии Федеральной политехнической школы Лозанны (Швейцария) и Института химии и технологии редких элементов и минерального сырья им. И.В. Тананаева Кольского научного центра РАН (Россия) Фабиана Кренингера, Иржи Ваничека и Сергея Антипова. Авторы предлагают усовершенствованную схему клеточной фильтрации, которая устраняет указанные проблемы и вводит внутренне согласованный механизм перехода между различными полуклассическими приближениями. Ключевая идея нового подхода: связать размер ячеек в фазовом пространстве с числом используемых траекторий. Вместо того чтобы фиксировать ширину ячеек заранее, авторы масштабируют их таким образом, что при увеличении числа траекторий ячейки автоматически уменьшаются, а плотность выборки центров ячеек расширяется.
Такое построение приводит к двум фундаментально важным пределам, которые придают методу особую элегантность и физическую осмысленность. В пределе бесконечного числа траекторий уточненная клеточная фильтрация строго переходит в исходный пропагатор Германа-Клука. Тем самым устраняется главный концептуальный недостаток стандартной схемы, не обладавшей этим свойством сходимости. В противоположном пределе, когда используется всего одна траектория, метод автоматически вырождается в хорошо известное приближение «оттаявшего» гауссова волнового пакета (thawed Gaussian approximation), впервые предложенное Эдвардом Хеллером в 1975 году. Таким образом, новая схема непрерывно связывает два полуклассических подхода, которые ранее рассматривались как концептуально разные методы.
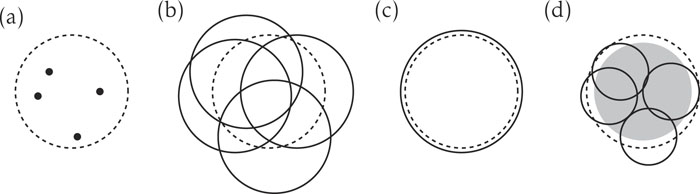
Изображение: сравнение стандартной и уточненной схем клеточной дискретизации для D = 1. Стандартная выборка: (a) Центры (точки) N = 4 гауссовых функций выбираются из функции Хусими начального состояния (пунктирный круг). (b) Соответствующие базисные функции (заполненные круги) имеют ширину, не зависящую от N. Предлагаемая выборка: (c) Для N = 1 нет свободы выбора центра, и метод согласуется с аппроксимацией размороженного гауссова распределения. (d) Для N = 4 центры гауссовых распределений выбираются из серого диска, их ширина равна половине ширины начального состояния, а ширина составляет 1/2 ширины начального состояния.
Авторы иллюстрируют преимущества предложенной схемы на ряде модельных задач, охватывающих как интегрируемые, так и хаотические динамические режимы. В качестве примера относительно регулярной динамики рассматривается модель коллинеарной молекулы NCO, в которой волновой пакет эволюционирует на возбужденной электронной поверхности. Расчеты временных автокорреляционных функций и соответствующих колебательных спектров показывают, что уточненная клеточная фильтрация практически идеально воспроизводит результаты полностью сходившегося пропагатора Германа-Клука при существенно меньших вычислительных затратах. В то же время стандартная фильтрация Филинова демонстрирует заметные искажения спектральных линий при недостаточно малых ячейках, что подчеркивает ее чувствительность к выбору параметров.
Особенно наглядно преимущества нового метода проявляются в случае хаотической динамики, где традиционные полуклассические методы испытывают серьезные трудности. На примере двумерного осциллятора, характеризующегося сильным хаосом, показано, что прямой расчет по Герману-Клуку приводит к неустойчивым и нефизическим результатам из-за взрывного роста вкладов отдельных траекторий.
Уточненная клеточная фильтрация, напротив, эффективно подавляет эти неустойчивости за счет адаптивного фильтрования и позволяет получить разумное описание кратковременной динамики, которая имеет наибольшее физическое значение, например, при расчете спектров с уширением линий. При этом статистическая ошибка метода оказывается существенно ниже, чем у стандартных подходов, даже при относительно малом числе траекторий.
Важным практическим результатом работы является также то, что вычислительная стоимость одной траектории в новом методе сопоставима со стоимостью в традиционном пропагаторе Германа-Клука и стандартной фильтрации Филинова. Это означает, что улучшение сходимости и устойчивости достигается не за счет усложнения динамики отдельной траектории, а за счет более разумной организации выборки фазового пространства и согласованного масштабирования параметров метода.
В целом представленное исследование демонстрирует, как переосмысление математической структуры полуклассических приближений позволяет не только повысить их вычислительную эффективность, но и прояснить связи между различными исторически сложившимися методами. Уточненная клеточная фильтрация фактически выстраивает непрерывный мост между приближением одного гауссова волнового пакета и полным ансамблевым описанием в духе Германа-Клука, предлагая единый параметр сходимости и устраняя произвольность выбора вспомогательных параметров.
Это делает метод особенно привлекательным для применения к большим и сложным молекулярным системам, где баланс между точностью и вычислительной реализуемостью имеет решающее значение: в фундаментальной химической физике (для упрощения описания временной эволюции молекулярных систем); в молекулярной спектроскопии (при моделировании и интерпретации экспериментальных спектров); в квантовой динамике (подход позволяет эффективно учитывать квантовые эффекты в рамках полуклассических методов); в вычислительной химии (для моделирования сложных молекулярных систем); в нелинейной динамике и теории хаоса.
Источник: Минобрнауки РФ